Trying my own double-slit experiment

This morning I decided I needed to do some double-slit experiments with lasers. To make my double-slit, I held two razor blades together and sliced a piece of aluminum foil.

I mounted my foil slide in some cardboard to hold it upright. I got a laser from a board game called Laser Maze.

And here it is with my double-slit slide in front of the laser. The interference pattern first discovered by Thomas Young (1773–1829) is clearly visible. I think the weird shape of my spots is due to my poor slit cuts.

It looks like the 13 brightest spots span a width of about 37.5mm. And my screen was about 3073mm away from the foil with two slits. To estimate how far apart my slits were, I stacked six razor blades. (That's all I had available.) It looks like 6 blades is about 3.5mm wide, so my two slits must be about 0.58mm apart.

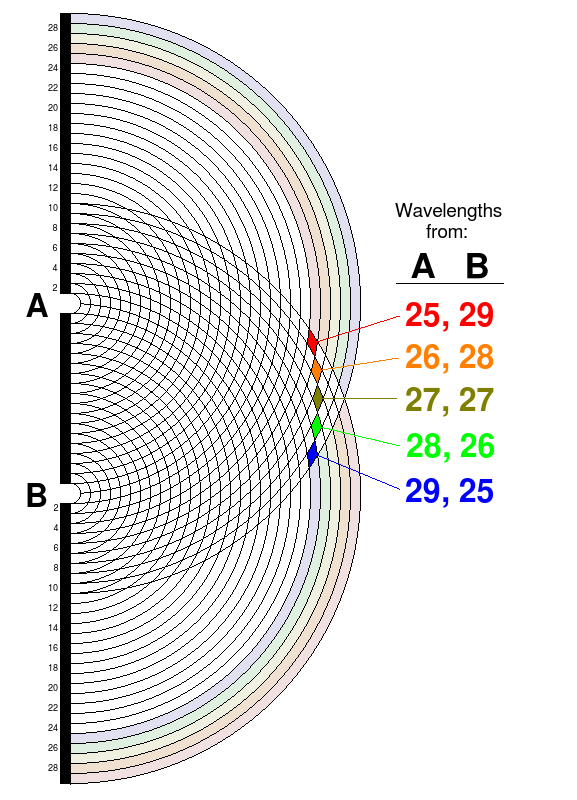
Next, I drew a bunch of circles to represent waves coming out of two slits. Let's say the lines represent troughs and the peaks are between the lines. So I filled in 5 regions where the waves reinforce each other to represent the bright spots on my paper. I counted how many wavelengths away each region was from each of the two slits. Obviously, the one in the middle is the same number of wavelengths away from both slits. And as you move away from the middle, you increment one and decrement the other. Makes sense.

Now, I think I'm ready to do some math. So I made the following diagram of my measurements:

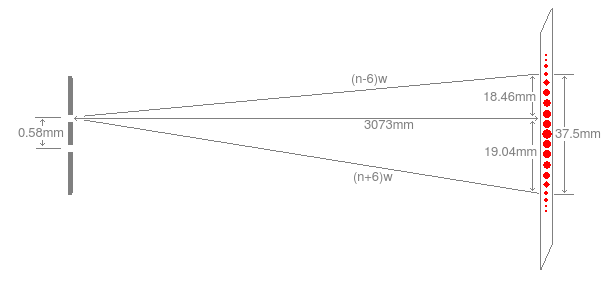
In this diagram, w is the wavelength of my laser, and n is the number of wavelengths to the center dot. I only showed the measurements for one slit since they are symmetric. Note that

Finally, I Googled it. (Really, I didn't even look this up until after I did the math and recorded my answer.) Google says the wavelengths of typical red lasers range from about 0.00063mm to 0.00067mm. So I was off by somewhere from 6.3% to 11.9%. Not too shabby! Given how poorly I estimated the distance between my slits, I think I was surprisingly accurate! I think if I worked on being more precise with my slits I could probably nail it.

So I can now add my witness to many others that I have personally validated light to behave like a wave. I can also now confirm that science really does have a basis for claiming to know the wavelengths of light. They aren't just making stuff up. I never really doubted, but it's still good practice to to validate stuff.

Being precise with explanations

But let's be careful about how we describe this. It is unfortunately very common for people to describe what is happening here by making an analogy with water. You've probably seen a lot of pictures like this:

This analogy is pretty good for explaining the concept of interference, but there is also something very incomplete about this explanation. If light were interfering like this, moving the screen closer to or farther away from the source would change the interference pattern. Let's try it:

Nope. The interference pattern is steady, even when the screen is moved closer or farther away from the source. What's going on? Are all those analogies with water too simplified? It looks like they are.

As accurately as anyone has ever been able to measure, the behavior of quantum particles seems to be accurately described by the Schrödinger equation. The Schrödinger equation describes a "wave function" in a continuous space of complex numbers. Don't let the word "complex" scare you. Complex numbers are not really very "complex". They just use two numbers to describe each point.

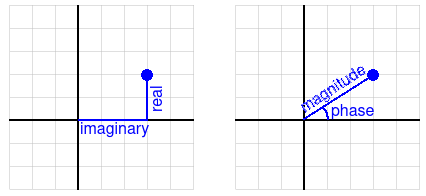
There are two ways to look at a complex number:
(1) You could describe it with a "real" and "imaginary" component, or
(2) You could describe it with a "magnitude" and a "phase".
But these are just two different ways of describing the same point.

You might think of the complex numbers in the Schrödinger equation like the water molecules that fill up a body of water. They are everywhere in the space, and they each affect their neighbors such that waves can pass through them. In water, waves are not fundamental entities. They are emergent phenomena that occur when water molecules interact with their neighbors. So are photons really even fundamental particles? Or are they some sort of emergent phenomena that occur in some kind of æther that fills all of physical space? No one even knows! But the standard model of particle physics treats them as fundamental, so if photons are just emergent waves, then most likely everything we think we know about in this universe is too ...and that's interesting!

Here is a Python script that uses the Schrödinger equation to simulate light passing through two slits: (This code was writtin by Arturo Mena López. I just touched it up a little for my experiments.)

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
@author: Arturo Mena López
Original source from: https://github.com/artmenlope
Mike Gashler pulled this code in October 2021 and made some minor modifications.

Script to simulate the passage of a Gaussian packet wave function through a
double slit with hard-walls (infinite potential barrier; the wave function
cancels inside the walls).

MIT License

Copyright (c) 2021 Arturo Mena López

Permission is hereby granted, free of charge,
to any person obtaining a copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation the rights to use, copy,
modify, merge, publish, distribute, sublicense, and/or sell copies of the Software,
and to permit persons to whom the Software is furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be
included in all copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND,
EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES
OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT.
IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM,
DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT,
TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE
OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
"""

from typing import List, Tuple
import numpy as np
import numpy.typing as npt
import matplotlib.pyplot as plt
import sys
from matplotlib.animation import FuncAnimation
from matplotlib.patches import Rectangle
import matplotlib.image as Image

def psi0(x:npt.NDArray[np.float64], y:npt.NDArray[np.float64], x0:float, y0:float, sigma:float=0.5, k:float=15*np.pi) -> npt.NDArray[np.float64]:
    """
    Proposed wave function for the initial time t=0.
    Initial position: (x0, y0)
    Default parameters:
        - sigma = 0.5 -> Gaussian dispersion.
        - k = 15*np.pi -> Proportional to the momentum.

    Note: if Dy=0.1 use np.exp(-1j*k*(x-x0)), if Dy=0.05 use
          np.exp(1j*k*(x-x0)) so that the particle will move
          to the right.
    """
    return np.exp(-1/2*((x-x0)**2 + (y-y0)**2)/sigma**2)*np.exp(1j*k*(x-x0)) # type: ignore


def doubleSlit_interaction(psi:npt.NDArray[np.float64], walls:List[Tuple[int,int,int,int]]) -> npt.NDArray[np.float64]:
    """
    Function responsible of the interaction of the psi wave function with the
    double slit in the case of rigid walls.

    Input parameters:
        psi -> Numpy array with the values of the wave function at each point
               in 2D space.
        walls -> A list of tuples, (left, top, right, bottom), specifying a rectangular wall

    Returns the array with the wave function values at each point in 2D space
    updated with the interaction with the double slit of rigid walls.
    """
    psi = np.asarray(psi) # Ensures that psi is a numpy array.

    # Cancel the wave function inside the walls of the double slit.
    for left, top, right, bottom in walls:
        psi[top:bottom, left:right] = 0
    return psi


# =============================================================================
# Parameters
# =============================================================================

L = 8 # Square well of width L*L. Shafts from 0 to +L.
Dy = 0.05 # Spatial step size.
Dt = Dy**2/4 # Temporal step size.
Nx = int(L/Dy) + 1 # Number of points on the x axis.
Ny = int(L/Dy) + 1 # Number of points on the y axis.
Nt = 400 # Number of time steps.
rx = -Dt/(2j*Dy**2) # Constant to simplify expressions.
ry = -Dt/(2j*Dy**2) # Constant to simplify expressions.

# Initial position of the center of the Gaussian wave function.
x0 = L/5 # near left-side
y0 = L/2 # vertically centered

v = np.zeros((Ny,Ny), complex) # Potential.

Ni = (Nx-2)*(Ny-2)  # Number of unknown factors v[i,j], i = 1,...,Nx-2, j = 1,...,Ny-2


# =============================================================================
# First step: Construct the matrices of the system of equations.
# =============================================================================
print('1/3) Setting up equations...')

# Matrices for the Crank-Nicolson calculus. The problem A·x[n+1] = b = M·x[n] will be solved at each time step.
A = np.zeros((Ni,Ni), complex)
M = np.zeros((Ni,Ni), complex)

# We fill the A and M matrices.
for k in range(Ni):

    # k = (i-1)*(Ny-2) + (j-1)
    i = 1 + k//(Ny-2)
    j = 1 + k%(Ny-2)

    # Main central diagonal.
    A[k,k] = 1 + 2*rx + 2*ry + 1j*Dt/2*v[i,j]
    M[k,k] = 1 - 2*rx - 2*ry - 1j*Dt/2*v[i,j]

    if i != 1: # Lower lone diagonal.
        A[k,(i-2)*(Ny-2)+j-1] = -ry
        M[k,(i-2)*(Ny-2)+j-1] = ry

    if i != Nx-2: # Upper lone diagonal.
        A[k,i*(Ny-2)+j-1] = -ry
        M[k,i*(Ny-2)+j-1] = ry

    if j != 1: # Lower main diagonal.
        A[k,k-1] = -rx
        M[k,k-1] = rx

    if j != Ny-2: # Upper main diagonal.
        A[k,k+1] = -rx
        M[k,k+1] = rx


# =============================================================================
# Second step: Solve the A·x[n+1] = M·x[n] system for each time step.
# =============================================================================
print('2/3) Solving over time...')
print(f'    0/{Nt}', end='\r')
sys.stdout.flush()

from scipy.sparse import csc_matrix
from scipy.sparse.linalg import spsolve

Asp = csc_matrix(A)

x = np.linspace(0, L, Ny-2) # Array of spatial points.
y = np.linspace(0, L, Ny-2) # Array of spatial points.
x, y = np.meshgrid(x, y) # type: ignore
psis = [] # To store the wave function at each time step.


psi = psi0(x, y, x0, y0) # We initialise the wave function with the Gaussian.

# One slit
# walls = [ # left,top,right,bottom,
#              (78,  0, 82,  76),
#              (78, 84, 82, 160),
#         ]

# Two slits
walls = [ # left,top,right,bottom,
             (78,  0, 82, 64),
             (78, 72, 82, 88),
             (78, 96, 82, 160),
        ]

# Two slits and barrier
# walls = [ # left,top,right,bottom,
#              (78,  0, 82,  64),
#              (78, 72, 82,  88),
#              (78, 96, 82, 160),
#              (86, 80, 90, 160),
#         ]

# Three slits
# walls = [ # left,top,right,bottom,
#              (78,   0, 82,  60),
#              (78,  68, 82,  76),
#              (78,  84, 82,  92),
#              (78, 100, 82, 160),
#              (78, 100, 82, 160),
#         ]

# Four slits
# walls = [ # left,top,right,bottom,
#              (78,  0, 82, 66),
#              (78, 70, 82,  74),
#              (78, 78, 82,  82),
#              (78, 86, 82,  90),
#              (78, 94, 82, 160),
#         ]

# Four slits and barrier
# walls = [ # left,top,right,bottom,
#              (78,  0, 82,  66),
#              (78, 70, 82,  74),
#              (78, 78, 82,  82),
#              (78, 86, 82,  90),
#              (78, 94, 82, 160),
#              (84, 80, 88, 160),
#         ]

psi[0,:] = psi[-1,:] = psi[:,0] = psi[:,-1] = 0 # The wave function equals 0 at the edges of the simulation box (infinite potential well).
psi = doubleSlit_interaction(psi, walls) # Initial interaction with the double slit.
psis.append(np.copy(psi)) # type: ignore # We store the wave function of this time step.

# Solve the matrix system at each time step in order to obtain the wave function.
for i in range(1,Nt):
    print(f'    {i}/{Nt}', end='\r')
    psi_vect = psi.reshape((Ni)) # We adjust the shape of the array to generate the matrix b of independent terms.
    b = np.matmul(M,psi_vect) # We calculate the array of independent terms.
    psi_vect = spsolve(Asp,b) # Resolvemos el sistema para este paso temporal.
    psi = psi_vect.reshape((Nx-2,Ny-2)) # Recuperamos la forma del array de la función de onda.
    psi = doubleSlit_interaction(psi, walls) # We retrieve the shape of the wave function array.
    psis.append(np.copy(psi)) # type: ignore # Save the result.

# Calculate the modulus of the wave function at each time step.
mod_psis = [] # For storing the modulus of the wave function at each time step.
for wavefunc in psis:
    re = np.real(wavefunc) # type: ignore # Real part.
    im = np.imag(wavefunc) # type: ignore # Imaginary part.
    mod = np.sqrt(re**2 + im**2) # We calculate the modulus.
    mod_psis.append(mod) # We save the calculated modulus.
    #mod_psis.append(re) # Replace the previous line with this one to see the real component
    #mod_psis.append(im) # Or this one to see the imaginary component

## In case there is a need to save memory.
# del psis
# del M
# del psi_vect

#%%
# =============================================================================
# Third step: We make the animation.
# =============================================================================
print('3/3) Animating...')

fig = plt.figure() # We create the figure.
ax = fig.add_subplot(111, xlim=(0,L), ylim=(0,L)) # We add the subplot to the figure.

img = ax.imshow(mod_psis[0], extent=[0,L,0,L], cmap=plt.get_cmap("hot"), vmin=0, vmax=np.max(mod_psis), zorder=1, interpolation="none") # type: ignore # Here the modulus of the 2D wave function shall be represented.

# Paint the walls
for left, top, right, bottom in walls:
    ax.add_patch(Rectangle((left*Dy,L-(top*Dy)), (right-left)*Dy, (top-bottom)*Dy, color="w", zorder=50))

# We define the animation function for FuncAnimation.
def animate(i:int) -> Image:
    """
    Animation function. Paints each frame. Function for Matplotlib's
    FuncAnimation.
    """
    img.set_data(mod_psis[i]) # Fill img with the modulus data of the wave function.
    img.set_zorder(1)

    return img, # We return the result ready to use with blit=True.


anim = FuncAnimation(fig, animate, interval=1, frames=np.arange(0,Nt,2), repeat=False, blit=0) # We generate the animation.

cbar = fig.colorbar(img)
plt.show() # Show the animation.

## Save the animation (Ubuntu).
anim.save('anim1.mp4', writer="ffmpeg", fps=20)

In the Schrödinger equation, the squared magnitue of the wave function corresponds with the probability that a photo-multiplier will detect a photon in that location. (A photo-multiplier is an instrument sensitive enough to detect a single photon.) Here is a plot of the magnitude of the wave function:

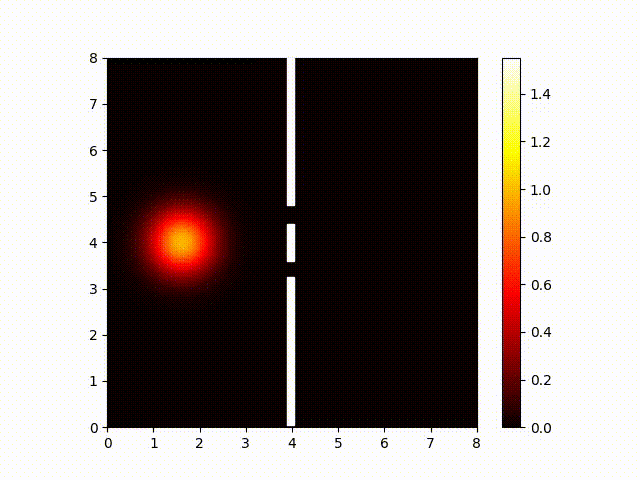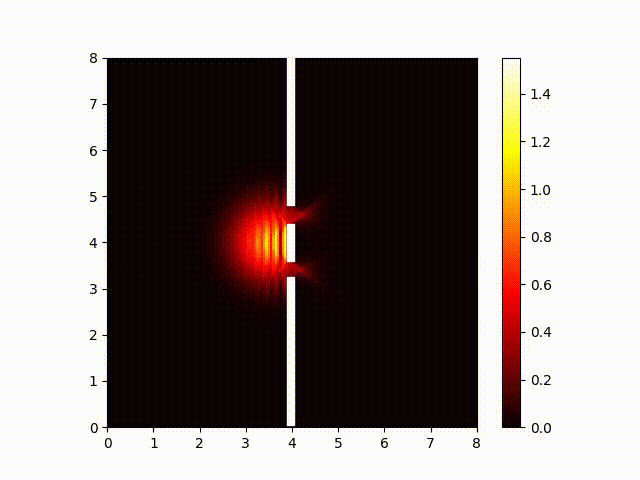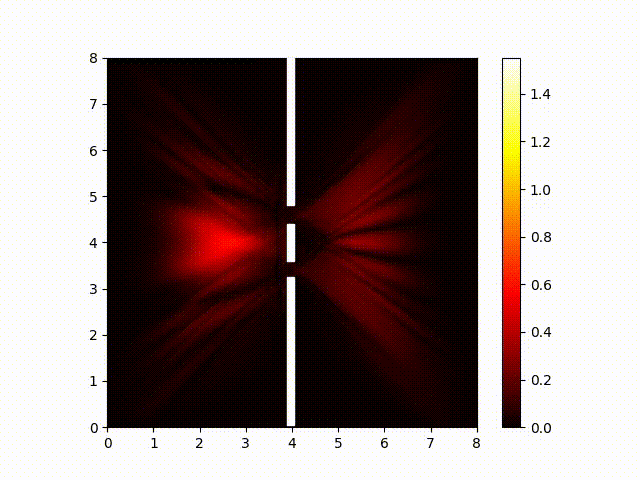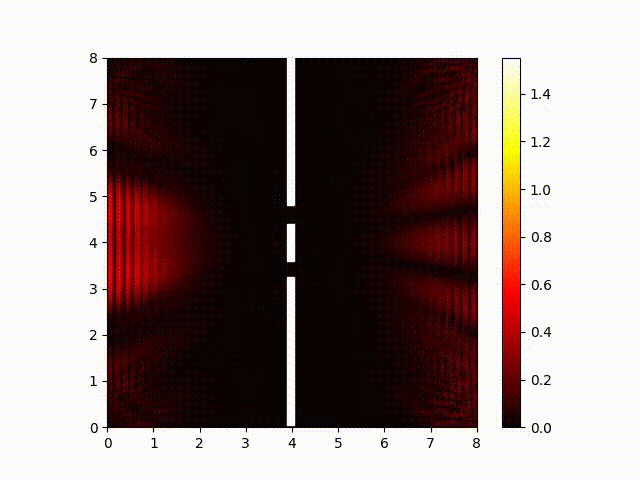
Notice how the interference pattern splays out like fingers to the right of the two slits. This is consistent with my experimental results showing that moving the screen did not have much effect on the interference pattern. So we've confirmed (at least in part) that the Schrödinger does a good job of predicting the behavior of light.

But the interference itself actually occurs in the real and imaginary components. That is, the real components of the wave function from the two slits sum together, and the imaginary components of the wave function from the two slits also sum together. So to see the waves interfere with each other, we need to look at the real and imaginary components. Here is a plot of the real component of the wave function:

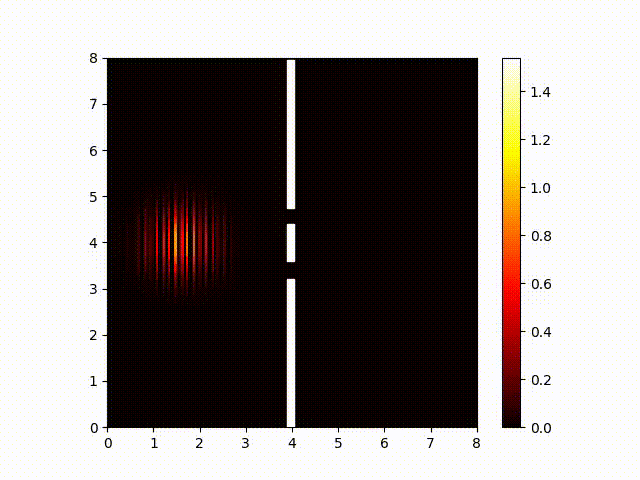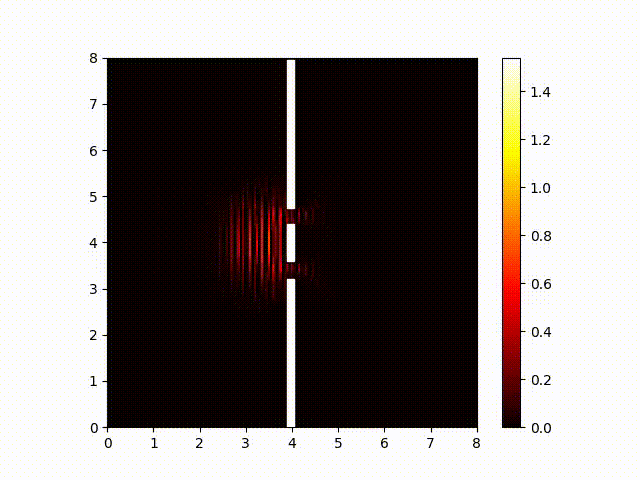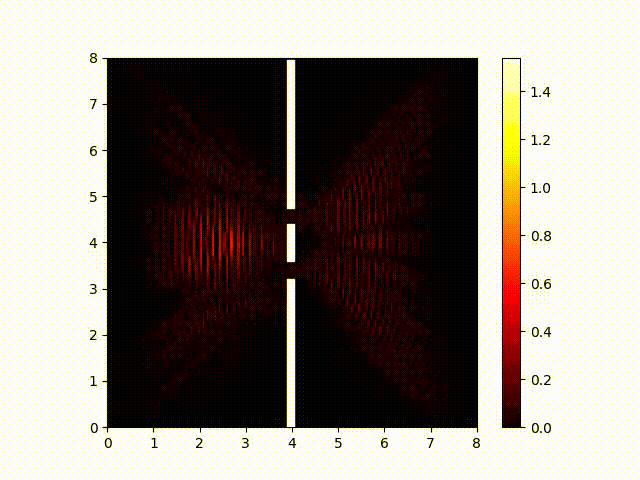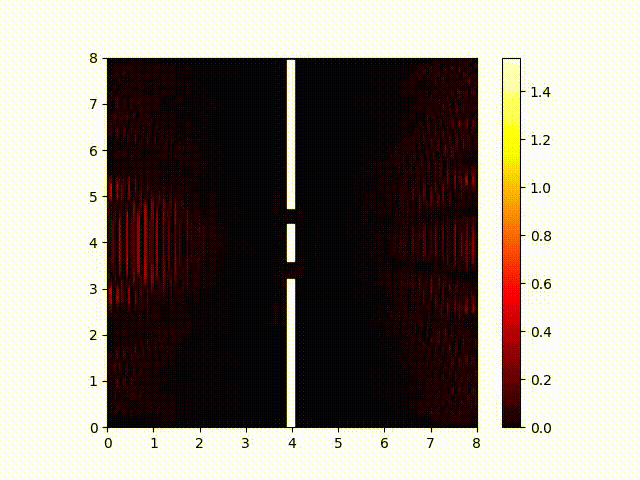
And for completeness, here is a plot of the imaginary component. (It looks pretty-much identical to the real component. The biggest difference you are likely to notice is that this animated image is probably out of sync with the "real" component one because your browser probably finished loading them at different times.) In both cases, the wave-length is smaller than a pixel, so what we actually see here is an aliassing pattern created from sampling the real and imaginary components at regular intervals.

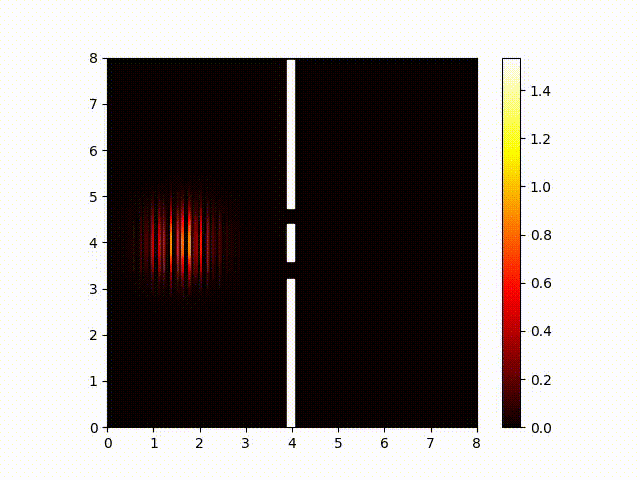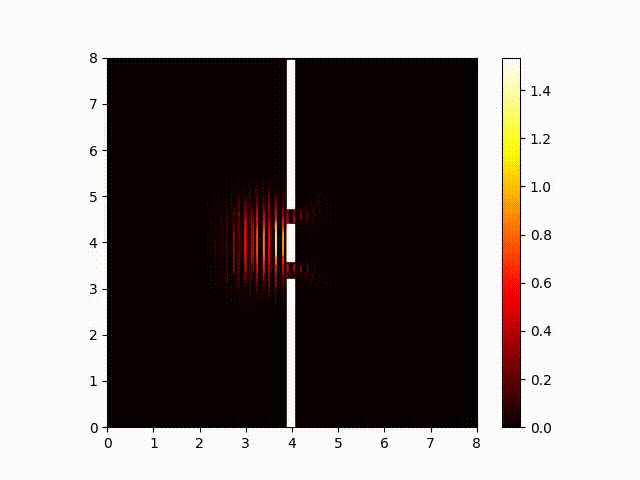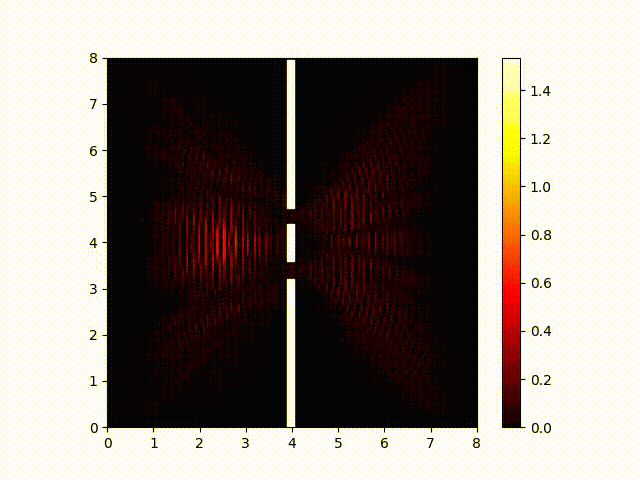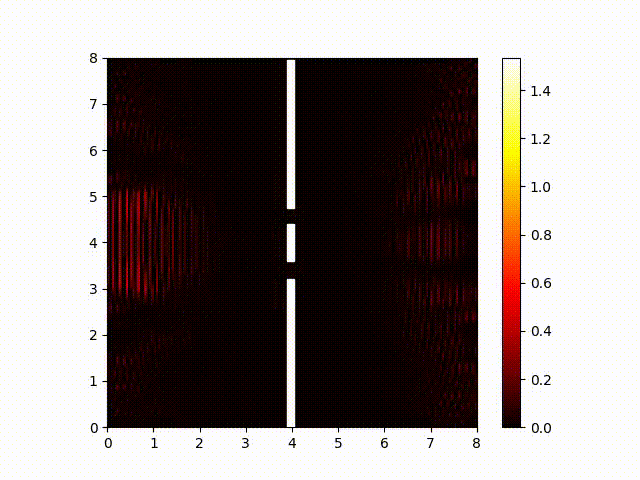
This is rather different from waves in water. In water, there is only one wave per slit, the waves interfere with each other in physical space, and we observe them in physical space. With quantum particles, there are two waves per slit, they interfere with the corresponding component of the wave from the other slit, and we observe only a probabilistic sampling of the magnitude, which is a combination of both components.

...but what exactly does it all mean? Why does the universe behave in this peculiar manner? And what can we learn from it?

Most of the explainers out there on the Internet make a big deal about what happens if you fire the photons one at-a-time. The photons arrive at the screen one at-a-time, but after enough of them accumulate on the screen we see an interference pattern.

But if you really think about it, that's exactly what happens anyway. All lasers shoot their photons one at-a-time. They just happen to shoot them at a rate we think of as rapid. To slow them down, quantum physicists just put a darkened lens or a partially-silvered mirror in front of the laser. Most of the photons are absorbed or reflected, but some small portion of them pass through. However, photons travel at the speed of light (obviously). The speed of light is really fast--really really fast. So no matter how rapidly you fire the photons, they still encounter the slits one at-a-time. Slowing down the rate and using a photo-multiplier to count individual photons doesn't actually change anything at all.

The bright spots in the interference pattern represent places where more photons have accumulated. But whether we shoot them rapidly or slowly, they still accumulate in the same places, every time. And it turns out that even if you send multiple quantum particles together, that doesn't even change where they accumulate either. It works with electrons, protons, neutrons, and any other quantum particle. It even works with entire molecules made up of many smaller quantum particles.

If we suppose photons travel in the form of individual particles, then the idea of a single particle passing through both slits and interfering with itself would certainly seem surprising. But we already know that's not what happens. Quantum particles are not like macro-scale objects. They occur only in quantized units. That seems somewhat particle-like. But all quantum particles are the same. That is not particle-like at all. And, it turns out, every properties we can possibly measure about quantum particles is quantized. That's definitely not how particles behave. Particles have continuous properties like position, mass, momentum, and velocity. With quantum particles, every property we can measure seems to be quantized at some level.

So how do we make any sense of the way quantum "particles" behave? Alas, science has not yet settled on the right interpretation, so the best we can do right now is compare several possible interpretations:

Interpretations

I'm not going to attempt to explain every interpretation here. Let's just review how the most common ones explain what happens when an individual photon is fired through a double-slit at a screen. But first I must warn you--these are all going to sound like really poor explanations. But there must be an explanation for this wierd behavior, and these are really the best explanations the brightest minds of modern times have been able to come up with:

Niels Bohr's and Werner Heisenberg's Copenhagen Interpretation is the most careful of the interpretations to avoid making wild assertions that cannot be measured. So in that sense it is probably the most scientific of the interpretations. Unfortunately, it also doesn't really explain much beyond what we can confirm experimentally. Basically, it says that the photon goes into a super-position of states. That means instead of acting like a particle, it turns into a wave-function that can simultaneously pass through both slits. The wave-function describes all possible positions for the photon. But significantly, the wave-function doesn't just encode possible positions. It describes all possible histories (including which path it took, which slit it passed through, and how it arrived at that position). All of these possible states (including the corresponding histories for each state) are maintained in the form of this wave-function as it simultaneously passes through both slits and interferes with itself, cancelling out possible states (and histories). When the photon strikes the screen, the wave-function starts getting increasingly complex as all the possibilities of interaction become increasingly chaotic. Then, at some (unspecified) moment, the wave function collapses. That basically means the universe gets tired of maintaining the complex wave function, so it randomly picks one position (with its corresponding history) and makes it real. At that moment, the photon is suddenly in one position on the screen and has only one history (even though that history reflects interference with other possible histories).

The von Neumann-Wigner Interpretation by John von Neumann and Eugene Wigner is a little more bold about making specific assertions. Confusingly, it is sometimes referred to as "the Copenhagen Interpretation" too, so it is important to be clear about which Copenhagen Interpretation we are referring to. I will only refer to this one the von Neumann-Wigner Interpretation. It says consciousness (not complexity) is what causes the wave-function to collapse back into a particle with a history. In other words, when the photon hits the screen the wave function just continues to become insanely complex, describing all possibilities of the photon interacting with various parts of the screen. It is not until a conscious observer contemplates the accumulation of photons on the screen that the wave functions finally collapse. At that moment, the universe picks one location and history for every photon. To put it another way, the whole universe is only real when conscious observers are looking at it.

Hidden variable interpretations try to preserve the intuitiveness of our universe by suggesting the wierd behavior of quantum particles is just due to some extra information they carry with them that we haven't yet found. The particles use this information to determine where they should appear when they strike the screen. These interpretations are very appealing to people who don't want to accept new and counter-intuitive rules in physics. Notably, Einstein was a proponent of these interpretations. Unfortunately, the more we learned about the behavior of quantum mechanics, the more information we started to realize would be needed for each particle to maintain, and the more complex the decision-making process would have to be when it finally struck the screen. So, hidden variable interpretations were forced to evolve to become just as wierd and complex as any of the other interpretations, suggesting particles carry entire memories with them and use some kind of little brains to make complex decisions.

Pop-sci woo interpretations (my name) emerge from arm-chair enthusiasts who are just too anxious to teach about the wierd behavior of quantum particles based on experiments they heard about, and not sufficiently careful to ensure they actually understand what those experiments have demonstrated. They typically teach that photons behave like particles when they pass through only one slit or when a conscious observer is watching, but behave like waves when no one is looking. Sometimes, they latch on to even more nuanced experiments, like the quantum eraser and resort to extreme interpretations such as there being some component of conscious intelligence that alters the behavior of quantum particles depending on its foresight, or rewrites the history of quantum particles based on whether conscious beings observe their effects.

Hugh Everett's many worlds interpretation invokes parallel universes to explain quantum phenomena. Schrödinger's wave-function is not encoded in any one universe, but rather is encoded in the many versions of the particle that are spread across many parallel universes. In other words, it says the quantum particle shoots off in all possible directions, one direction in each of the parallel universes. In some universes, the photon passes through one of the slits. In some universes, the photon passes through the other one. And in several universes, the photon just strikes the slide somewhere between the two slits. Yet, even though these photons are all in different universes, they still interact with each other like neighboring molecules in a sea of water, and resulting in the interference patterns that occur with waves. The reason we ultimately find only one particle hitting the screen at-a-time is because we just happen to be in the one universe where the particle ends up in that one location. If the many worlds interpretation is right, there are parallel versions of ourselves in other universes looking at the screen and finding the same particle in other possible locations on the screen.

Why each of these interpretations looks wrong

In my personal opinion all of these interpretations are downright awful. None of them are very intuitive, and all of them suggest some pretty wild things about our universe. So what is to be done? Well, let's try to be good scientists about it. Instead of just championing the one that seems the least offensive to us, or that works best with our world-view, let's try to be open-minded and see if we can find some reproducible experiments to help us narrow down the set of possibilities. (And as we do that, let's also try be very careful not to suppose our set of possibilities is necessarily complete, or that any of the various interpretations cannot be adjusted or refined. Our priority should always be learning before teaching.)

Fortunately, one of these interpretaions has already been ruled out for us. In 1964, John Bell did some experiments that disproved most hidden variable interpretations. If you were rooting for a hidden variable interpretation, then it might be worthwhile to take the time to read more about it. But these days few quantum physicists even seriously consider any hidden variable interpretations, so I think it's pretty safe to discard that one and move on.

Next, let's see if we can do something about the Pop-sci woo interpretations. If we consult the Schrödinger equation, we can see that it predicts light will behaves as a wave even when it passes through only a single slit.

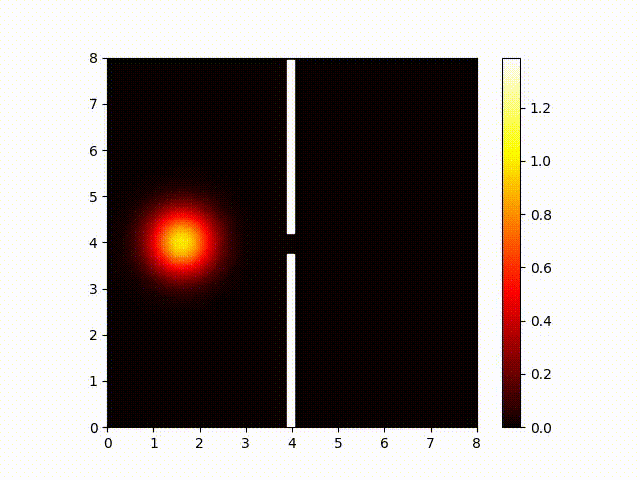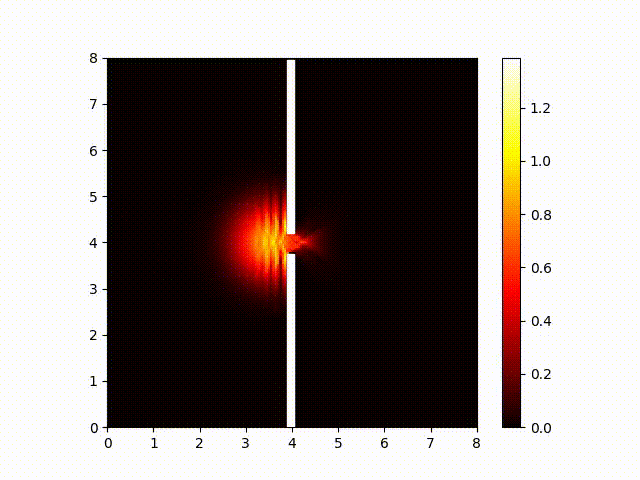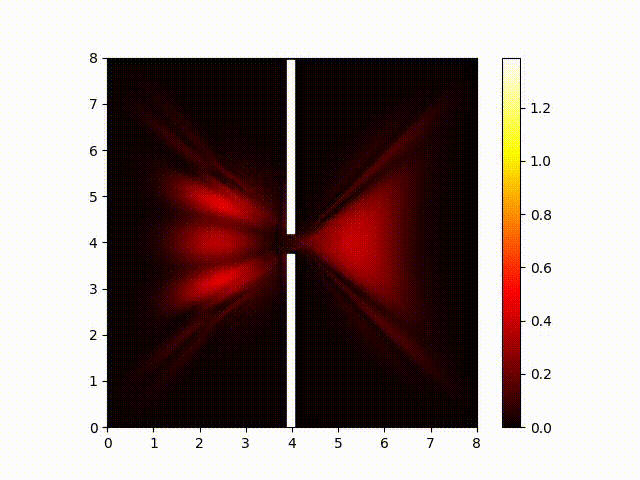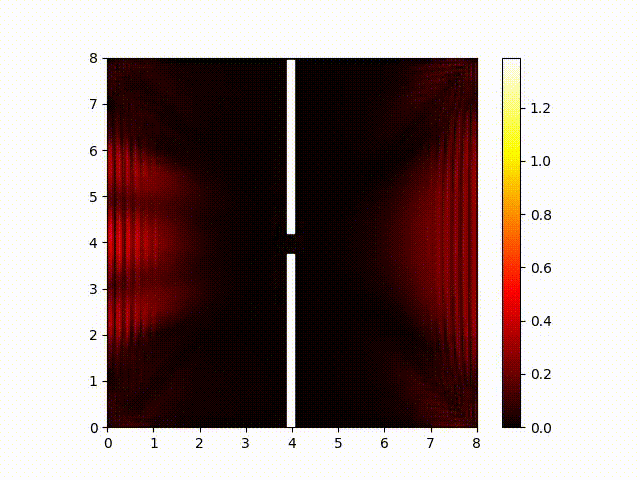
This differs from the Pop-sci woo interpretation, which suggests light sometimes behaves like a particle. This is something we can easily test, so let's find out which is right. Here is a picture of my single-slit slide:

Notice my single slit is vertical (not horizontal). And here's the pattern the photons make when they pass through this slide. Notice that the photons spread out out horizontally (not vertically).

What does this mean? It means photons never really start behaving like particles. Particles would make a pattern shaped the same as the slit. (That is, it would be vertical rather than horizontal.) Waves would continue to behave according to the Schrödinger equation. And that's what we observe.

I suspect the idea that light sometimes behaves as a "particle" comes from a misunderstanding of wave-particle duality. Yes, Einstein did received a Nobel Prize for recognizing light had both wave-like and particle-like properties. But contrary to the interpretations of arm-chair physicists, photons do not magically switch back and forth between being waves or particles depending on how many slits they are passing through. To a quantum physicist, the term "particle" does not mean it behaves like a tiny billiard ball. Let's elaborate:

Billiard balls can come in many different sizes. Photons are all the same size and have zero mass. That's not like a tiny billiard ball at all. Billiard balls can travel at any speed. Photons can only travel at the speed of light. So really, there are no such thing as tiny "particles". That's just a term physicists use to refer to quantized waves that are not really like little balls at all.

So we see that photons don't change their nature or behavior when there are two slits. They always seem to travel the way the Schrödinger equation predicts. They are always waves, just quantized waves. So we can rule out the Pop-sci woo interpretation. It's just wrong. But do photons change their behavior when they interact with macro-scale objects? Let's test that next...

So next, I tried to "collapse the wave function". If Bohr's Copenhagen Interpretation is correct, then interaction with a macro-scale object should cause the quantum wave function to collapse, causing the light to start behaving as quantized photons instead. But as you can see, putting large objects in the path of the wave didn't actually cause it to collapse.

An astute observer might say, "well, maybe the photons that impact your finger do collapse, but all the ones that miss your finger just behave normally". However, that supposes the light is already quantized into photons. Bohr's Copenhagen Interpretation suggests light travels as the entire wave function, and doesn't become a quantized particle until that wave function collapses. In other words, my finger was interacting with a portion of the wave function of every photon that emanated from my laser! If that was sufficient to cause the wave function to collapse then it should have collapsed them all. But it didn't.

It seems pretty clear from these experiments that interaction with macro-scale objects does not cause photons to change form. So that's not great for Bohr's Copenhagen Interpretation. But does consciousness have an effect?

Well, I just happen to be conscious, so I can test this too! (I can't prove I am conscious to you, but this experiment is pretty simple to reproduce if you would rather do it yourself.) So as a conscious observer, I watched my laser interact with my finger, and it still didn't cause the wave function to collapse. I took pictures too. Even if you don't trust that I am conscious, you can see the pictures I took, so technically your viewing of the pictures should cause a superposition of universes to collapse into one where my laser light started behaving like a bunch of particles. But it didn't. So it's not looking great for the von Neumann-Wigner Interpretation either.

I tried collapsing the wave function in every imaginable place. I touched the laser before the slits, after the slits, in front of just one slit, near the screen, near the laser, and so forth. And I carefully watched the interference pattern the whole time. It never stopped occurring.

Well, completely blocking one slit killed the interference pattern, of course, but it still spread out as waves do with a single slit. And blocking the whole laser source stopped all light from reaching the screen. But nothing I did ever caused the quantum wavefunction to collapse in any sort of manifestation of quantum weirdness.

Just to be sure, let's try a different setup: So I got out the partially-silver mirror.

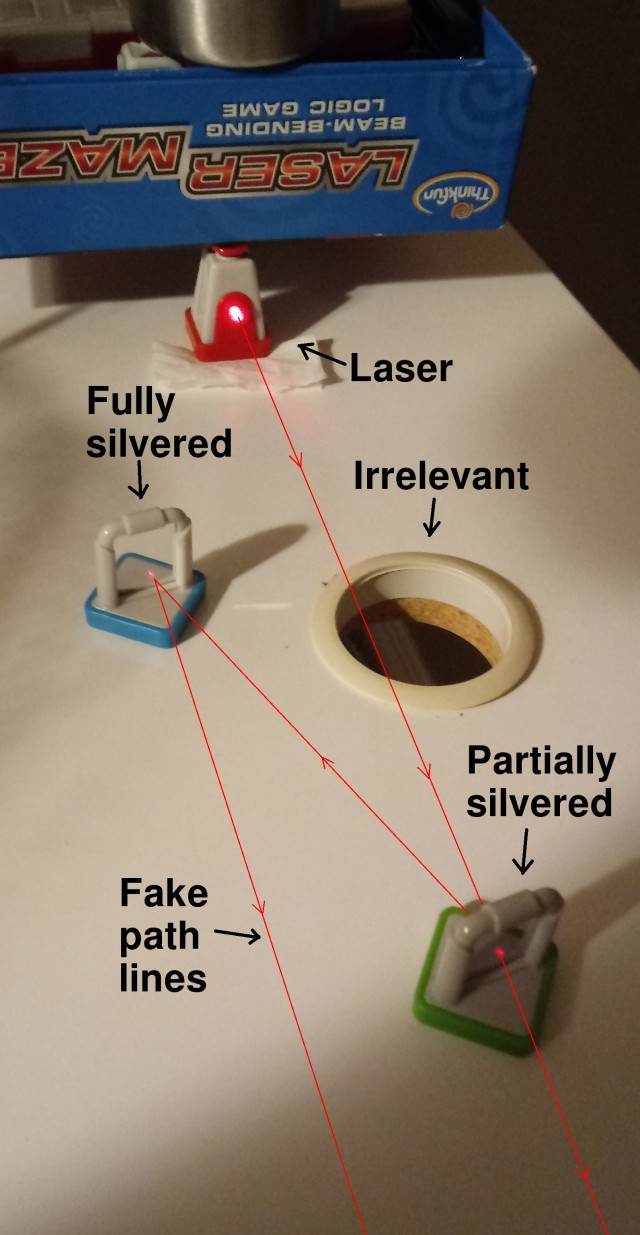
As expected, this made two dots on my screen. For a while, I spent considerable effort aligning the dots and trying to get them to interfere with each other, but since I couldn't get the two beams close enough to being parallel, the interference pattern was always too tiny to discern.

According to Bohr and von Neumann, the quantum wave function simultaneously propagates down both pathways. If the wavefunction along either pathway is "observed", it collapses and no interference patterns should occur along the other pathway. So next, I put my double-slit slide in front of the other pathway.

When I blocked the dot with my hand, the interference pattern in the other beam persisted. But, one might object, my hand isn't conscious! Since this is for science, I did something you're never supposed to do and I looked directly into my laser! I had my children carefully watch the interference pattern on the other beam as conscious observers while I did this. They say it never changed. I also video-recorded it, and my recording confirms what my children said. No collapse! (Also, my eyes bothered me after doing that, so I hope you appreciate it!)

Supposedly, Complementary Metal Oxide Semiconductor arrays can be made sensitive enough to detect individual photons. I doubt the one in my phone camera is anywhere near that sensitive, but I also have a hard time imagining the quantum wave function exercises sufficient intelligence to evaluate the quality of my phone. So here is video of my phone failing to collapse the quantum wave function. I personally watched the interference pattern as I did this, and it never collapsed.

So next, I put my double-slit foil in front of the partially-silvered beam splitting mirror. Now the quantum wavefunction follows four separate paths, and I get two unique interference patterns.

In this picture, the interference pattern in the lower-right is not very clear, but it was very clear in real life. Maybe I'll redo that picture sometime, but there was definitely an interference pattern in both of them. Meh, you can redo it if you want to.

So then I repeated all my experiments in every location, with children and cameras and every combination of intervention I could think of. I tried adding another mirror that projected one of the paths onto my ceiling. The idea here was to make one of the paths longer, and also make the wavefunction along one pathway go through an extra transformation, hoping to wear down the universe with more complexity while I observed the shorter pathway. But still I couldn't get that darn interference pattern to go away.

It looks pretty clear to me that consciousness does not cause wave functions to collapse any more than interaction with macro-scale objects. In fact, it looks to me like photons never really change their form at all. ...so this brings us to Everett's Many Worlds Interpretation.

Many Worlds is the only one of these interpretations that predicts the photons never change form. And so far it is the only one that consistently predicts all of the behavior I have just observed. So what's wrong with the Many Worlds Interpretation?

Resources. Can you think of anywhere in all of nature where resources are unlimited? I cannot. And can you think of anything more wasteful of resources than cloning entire universes? I mean, where does all the time, space, energy, and matter necessary to do that even come from? And moreover, the Many Worlds interpretation doesn't just suggest there are a lot of universes. It suggests a near-infinite number of universes must pop into existence every time a particle moves! Now, just think about how many moving particles there are in the entire universe, and try to imagine how many total universes that spawns in just a fraction of a second? Now, imagine that exponentiating for the last 13.8 billion years! That's an utterly unfathomable cardinality of universes! Yeah, that's pretty crazy!

So here's the situation we find ourselves in: Most interpretations are demonstrably wrong. And the only one that is consistent with my experimental results is absolutely bonkers! So now what?

Resolution

How could such great minds as Bohr, Heisenberg, Schrödinger, von Neumann, and Wigner be mistaken? It turns out the matter is not as controversial as some people like to pretend it is. It's true that Bohr, Heisenberg, Schrödinger, von Neumann, and Wigner all thought consciousness was the cause at some point. But most of them ended up changing their minds. The only reason such silly ideas are still repeated is because people with agendas continue to use the names of these great scientists who abandonded that idea. Here's a SpaceTime episode that explains it pretty well: (In particular, pay attention around time 10:34, when he points out how the founding fathers of quantum mechanics changed their minds.)

One pattern I've observed is that people who are adamant about the Copenhagen Interpretation or the von Newmann-Wigner Interpretation are often trying to push the notion that consciousness is fundamental rather than emergent. But it is easy to show that consciousness is emergent. We can suppress consciousness with drugs. If consciousness were fundamental, drugs would only inhibit the body. Anesthetized people would wake up with memories of being unable to reach their chemically-disabled bodies.

In order to further test the von Neumann-Wigner Interpretation, scientists have programmed robots to perform the double-slit experiment. The robots obtain exactly the same results as conscious humans. Nevertheless, some people really really want consciousness to be fundamental, even if the originators of the idea have abandonded it. They insist that the robot just gets pulled into a super-position with the quantum particle until a conscious observer finally contemplates the results, and then the universe decides which robot history to make real. In other words, these peoples' minds are made up. They will accept no other answer besides fundamental consciousness being responsible, so there is no use trying to tell them otherwise.

My own survey of physicists who actually work in this domain indicates that they pretty consistently take one of two positions: Either they (1) embrace Many Worlds, or (2) they think no good explanation has yet been found. So if we want an explanation right now, it seems that Many Worlds is the only viable option.

Now, let be clear: I'm not suggesting we get married to Many Worlds. I'm not suggesting we embrace it as some kind of new religion. I'm just saying let's tentatively see if we can find a way to tolerate it, so we can have an explanation to work with, just until something better comes along.

Let's consider another concept that is much less controversial: time. Do you accept that time is a real thing? Of course you do! Everyone is familiar with time. Maybe we don't know exactly what time is, but it's clearly a real phenomenon.

So, let's compare what the Universe is like right now to what the Universe was like exactly one second earlier. They're pretty similar, right? In both universes, you were reading this article. The weather probably hasn't change much in just one second of time. Almost everything was the same, except with slight variations. To be specific, there was about one second worth of differences.

Now, consider exactly how many different universes occurred between in the one second time-interval. If we suppose a unique universe occurred every Planck-time, that's 5.4*10⁴⁴ very similar universes! Well, that's pretty absurd, isn't it? Where did all those universes come from? What resources were used to spawn so many extremely similar universes? Shall we throw out the entire concept of time just because it doesn't make sense? Of course not! We have abundant evidence time is real. We accommodate time because we absolutely have to--it's all around us. We simply cannot deny it. And likewise, we are starting to find a lot of evidence that the multiverse is real too. In fact, you can test it for yourself just as I did. Interference patterns are the evidence that has convinced quantum physicists that there are Many Worlds.

Perhaps, you might object, "Wait! the passage of time doesn't produce different universes. It's all just one universe at different times!" Well, if time is something the Universe can vary over, perhaps there could be other dimensions or variables it the Universe can vary over as well. You see, Many Worlds isn't necessarily saying the Universe is duplicated. That's just an awkward attempt to explain a difficult concept. But you already accept that the past is a real phenomenon--or at least, it was. Well, the multiverse need not be any more "real" than the past. It merely needs to be something that has an influence on the present.

In my opinion, saying there is an "infinitude of universes" gives the wrong impression. The makes it sound like there is some completely unfamiliar cloning of universes occurring. A much better way to explain it is to simply suggest there are probably additional dimensions. Perhaps, every place in these dimensions could be termed a different universe, but it's probably more reasonable to think of it as a slightly varied place in the same universe, much as the present is just a variation of the recent past.

There must be at least 3 additional dimensions because I can get an interference pattern in any direction that I point my laser. But are there more than three? I hope so. Quantum computers depend on it. But no one has really worked out the details of how the multiverse works, yet. All we know is we have found a hint of it. And that's not stupid at all. That's exciting! That means we have found new frontiers out there for science to explore!

The Schrödinger equation came out in 1926. That's almost 100 years ago! And we still haven't made very much progress on this frontier. Apparently, it's a very difficult frontier to advance. But won't it be amazing when we finally start to understand what we have discovered?