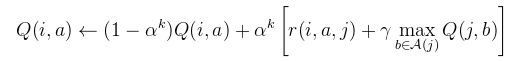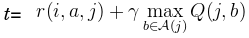Q-learning
- Using your favorite search engine, find a simple tutorial on Q-learning.
Read the tutorial.
- Implement Q-learning.
Here is some pseudocode for one iteration of Q-learning.
Your program will call this in a loop until it converges:
// Pick an action
Let Q be a table of q-values;
Let i be the current state;
Let ε = 0.05;
if(rand.nextDouble() < ε)
{
// Explore (pick a random action)
action = rand.nextInt(4);
}
else
{
// Exploit (pick the best action)
action = 0;
for(int candidate = 0; candidate < 4; candidate++)
if(Q(i, candidate) > Q(i, action))
action = candidate;
if(Q(i, action) == 0.0)
action = rand.nextInt(4);
}
// Do the action
do_action(action);
Let j be the new state
// Learn from that experience
Apply the equation below to update the Q-table.
a = action.
Q(i,a) refers to the Q-table entry for doing
action "a" in state "i".
Q(j,b) refers to the Q-table entry for doing
action "b" in state "j".
Use 0.1 for αk. (Don't get "αk" mixed up with "a".)
use 0.97 for γ (gamma).
A(j) is the set of four possible actions, {<,>,^,v}.
r(i,a,j) is the reward you obtained when you landed in state j.
// Reset
If j is the goal state, teleport to the start state.
Here is the equation that you will implement at the core of your Q-learner:
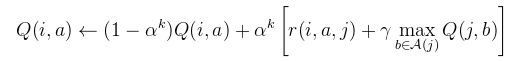
.
- Implement a simple grid-world.
Use dimensions of 20 wide and 10 high. There are 4 possible actions: {left, right, up, down}.
Start in one corner. Place a reward in the opposite corner.
Place a wall of penalty states with a small hole through which the agent can pass somewhere between the start and goal states.
Use some probability that actions will cause unintended behavior.
Use Q-learning to learn a policy for solving this problem.
(Your Q-table will require 20*10*4=800 elements.
Initialize them with zeros, then iteratively apply Q-learning until your Q-table converges to represent a good policy for this game.)
- Print your policy at periodic intervals to the console while it learns.
Use "#" to indicate a penalty state, "G" to indicate a goal, and the characters "<,>,^,v" to indicate left, right, up, and down for the policy in all other states.
Example:
> > v v v v v v < < # > > > > > > > > G
> v > v v v v v v < # > > > > > > > ^ ^
> > > > > v v v v < # > > > > > ^ ^ ^ ^
> > > > > v v v v < # > > > > > ^ ^ ^ ^
> > > > > > v v v < # > > > > ^ ^ ^ ^ ^
> > > > > > > > v v # > > > ^ ^ ^ ^ ^ ^
> > > > > > > > > > > > > ^ ^ ^ ^ ^ ^ ^
> > > > > > > > > > > > > ^ ^ ^ ^ ^ ^ ^
> > > > > > > > ^ ^ # > > > ^ ^ ^ ^ ^ ^
> > > > > > > > ^ ^ # > > > ^ ^ ^ ^ ^ ^
> > > > > > > > ^ ^ # > > > ^ ^ ^ ^ ^ ^
> > > > > > > ^ ^ < # > > > ^ ^ ^ ^ ^ ^
> > > > > ^ ^ ^ ^ < # > > > ^ ^ ^ ^ ^ ^
> > > > ^ ^ ^ ^ ^ < # > > > ^ ^ ^ ^ ^ ^
S > > ^ ^ ^ ^ ^ ^ < # > > > ^ ^ ^ ^ ^ ^
- If you are taking the graduate scetion of this class,
if your program is executed with an optional command-line parameter, "nn",
use a neural network to implement your Q-table instead of some other data structure.
You can use the neural network from previous assignments.
Some fiddling may be necessary to find a suitable number of layers,
and other meta-parameters to get it working.
The neural network may require many more iterations for convergence to occur.
I recommend using two inputs {x,y} and 4 outputs {q-left,q-right,q-up,q-down}.
Here is an example that makes a neural network with the topology 2->16->4:
Random rand = new Random(1234567);
NeuralNet nn = new NeuralNet();
nn.layers.add(new LayerTanh(2, 16));
nn.layers.add(new LayerTanh(16, 4));
nn.init(rand);
To refine your neural network, call "trainIncremental(in, out, 0.03)", where "in" is your input vector, "out" is your output vector, and 0.03 is a reasonable learning rate.
Remember to train it using values that have been normalized to fall approximately in the range [0,1].
To make a prediction with your neural network, call "forwardProp(in)", and it will return the vector of 4 Q-values for the state you specify.
If you only want to refine one of the 4 q-values, then use the predicted values for the other 3 q-values when you call "trainIncremental".
That way, it will only attempt to change the one q-value for which it is making different predictions.
So, let
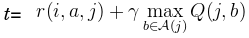
Then, instead of doing Q(i,a)=(1-α)*Q(i,a)+α*t, do
double[] prediction = nn.predict(i);
double[] copy = Vec.copy(prediction);
copy[a] = t;
nn.trainIncremental(i, copy); // This line updates the neural net
- Click on the "Project submission" link on the main class page to submit your archive file.
If you have any difficulties with the submission server, please e-mail your submission directly to the grader.
|